Understand and master Froude theory on screew propeller, and wind turbines betz limit:

To understand Theory Froude, the notion of momentum must be mastered, because it is on the balance of momentum that the Froude theory is based ..

Froude method uses the equations of conservation of momentum to determine the performance of a propeller viewed as a uniformly loaded disc having an infinite number of blades. The axial induced velocities can thus beings evaluated

• we set the following assumptions, according to which:
  • The rotation of the flow is neglected
  • The fluid is incompressible
  • The flow out of the duct through the disc is undisturbed
  • The pressure at infinity upstream and downstream is equal to the static pressure
    flow
  • Air passes through the rotor without friction

The disc acts as a brake, opposing force T to the fluid stream. This force can be considered as the result of the pressure diference between the upstream and downstream of the disc.

The continuity equation tells us that, to maintain a flow even if the speed decreases section must increase. If we observe the flow of the fluid stream passing through the disk, so we see the section increased by the braking of the fluid..

Watch our propeller in a control volume larger than the vein through the propeller. We find that the expansion of vein can only be done if a certain amount of fluid is evacuated from the volume control..

 

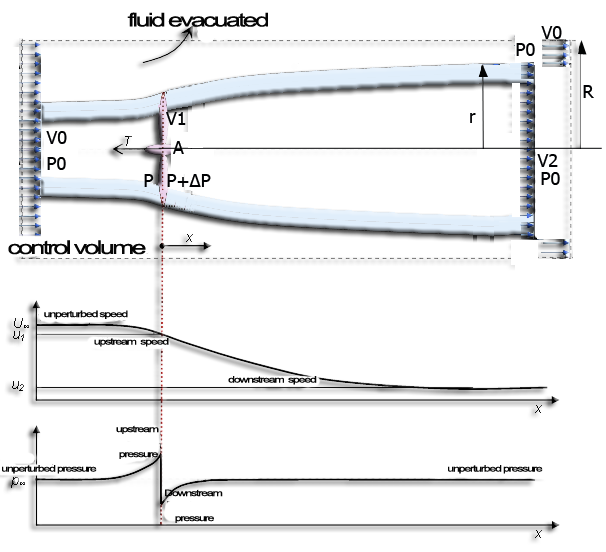
lthe continuity equation allows us to calculate the volume removed from the control zone per second (volume flow Q in m3/sec),

 

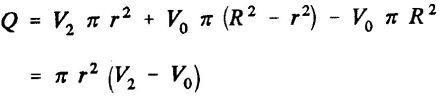
Q is the volumetric flow discharged from the volume control. From the theorem of momentum, the thrust, T of the propeller is obtained, that is to say the variation of the amount of movement between the sections 2 and O, whose projection on the horizontal axis indicates thrust :

the derivative of the momentum versus time :

Momentum out "M_2" volume control in Section 2 =

Total amount of movement "M_1" within the volume control = Momentum in the volume entry - momentum laterally Evacuated=

Therefore, the axial force of the fluid on the rotor becomes(T=M_2-M_1):

One can also express the axial force of the fluid on the rotor T, according the result of the static pressure which is exerted on the surface of disc:

where A is the surface of the disc swept by the propeller and Dp, the pressure difference across the disc. Using Bernoulli's equation, we obtain:

pressure difference O to 1 upstream, and:

pressure difference 2 to 1 downstream.

 

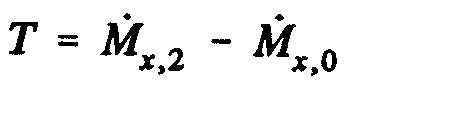
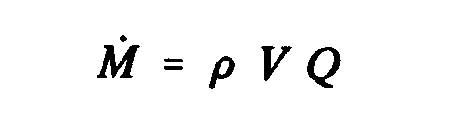
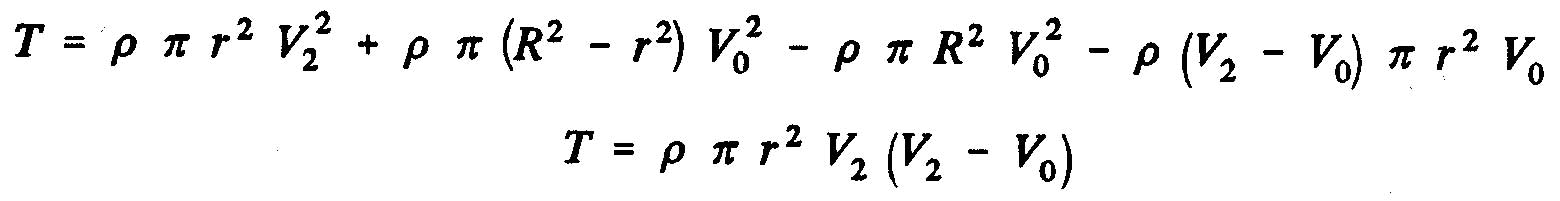
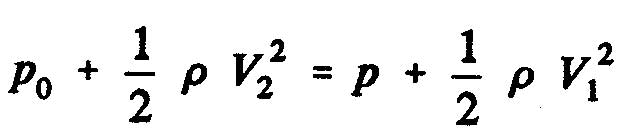
The static pressure difference between the upstream and downstream sides of the disk of the propeller as the expression:

From the continuity equation:, can be derived:

and consider the speed of the flow through the disk as an arithmetic average of the velocities upstream and downstream of the propeller:

The speed of the air flow through the rotor is the average of the two speeds upstream and downstream of the rotor. Is called induced velocity w, increasing speed at the propeller disk:

where "a" represents the axial interference factor.

 

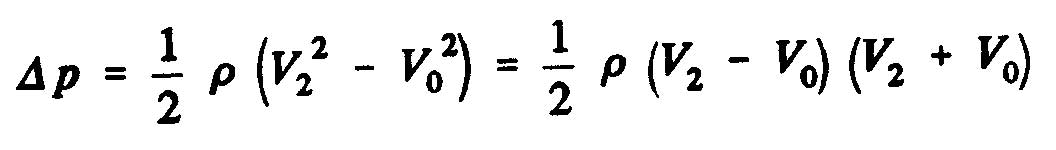
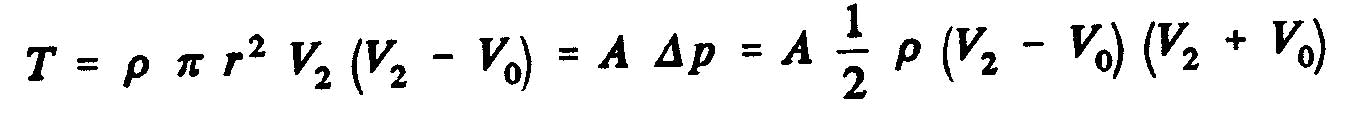
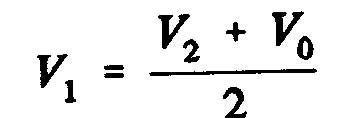
Now, if we consider the expression:, the axial force exerted on the disc of the impeller is:

The power extracted from the wind :

The power coefficient is defined as the ratio between the available wind power and the power extracted:

Inserting the axial interference factor "a", defined as the fraction of the decrease in wind speed between the free-flow upstream of the rotor and the rotor plane :

• V=(1-a).V0

Using the equation::

• V1=(1-2a).V0

knowing:

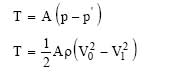
substituent V and V1, is obtained :

The expression of Cp becomes

The maximum theoretical power coefficient, known as the Betz limit can be obtained by taking the derivative of Cp versus: a=0 ,

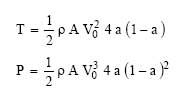
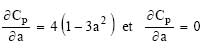
this gives :

The maximum efficiency for an ideal turbine is approximately 59.3%. In practice, this performance is never done because of the following effects :

• The air flow has a rotating component due to the rotation of the rotor.
• The drag force is never zero due to friction.
• The propeller contains a finite number of blades.

This simple one-dimensional model does not describe the rotating airflow, though it sets some basic concepts in the work of wind turbines.
So that the propeller extracts energy from the wind, the speed thereof must decrease when passing through the propeller. An ideal machine must slow down the wind speed of 2/3.
From the continuity equation (1), the section of the air swept by the wind increases from upstream to downstream. For an ideal wind turbine, the cross-sectional area of the flow upstream is 2/3 that of the rotor, and the latter is half that of the downstream section. Finally, the extraction of all available wind energy is virtually impossible, in practice, the performance of wind turbines does not exceed 45 %.

 

The theory froude gives us the axial induced velocity. It will be linked to the theory of the blade element to give a decomposition of the induced velocity in tangential and axial induced velocities necessary for the prediction of the incidence angles and the geometry of the blades..

Bibliographic references propeller

Products | Store | My Mecaflux | My Licences | Key generator | My cart | Contact

Copyright © 2024 Mecaflux. All rights reserved. last update 06 february 2024
Terms of sale| Privacy and cookies